《大话数据结构》知识点汇总+算法代码总结-xiaoming

注意事项

在使用malloc进行结构体的内存申请时注意申请的对象

例如：

typedef struct StackNode
{
	int data;
	struct StackNode* next;
}StackNode, * LinkStackPtr;

LinkStackPtr p = (LinkStackPtr)malloc(sizeof(StackNode));
LinkStackPtr p = (LinkStackPtr)malloc(sizeof(LinkStackPtr));

申请内存时，malloc(sizeof(StackNode)) 分配的内存大小是 StackNode 结构体的大小，而 malloc(sizeof(LinkStackPtr)) 分配的内存大小是指向 StackNode 结构体的指针的大小。

在使用 free(p) 进行内存释放时，使用 malloc(sizeof(LinkStackPtr)) 分配的内存，因为 LinkStackPtr 实际上一个指向 StackNode 结构体指针的内存块，而不是指向实际数据的内存块，因此在进行释放时会出错。

1. 线性表

1.1 线性表的定义

线性表：零个或多个数据元素的有限序列

线性表元素的个数（n≥0）定义为线性表的长度，当n＝0时，称为空表。
优缺点：
- 优点：
  - 无须为表示表中元素之间的逻辑关系而增加额外的存储空间
  - 可以快速地存取表中任一位置的元素
- 缺点：
  - 插入和删除操作需要移动大量元素
  - 当线性表长度变化比较大时，难以确定存储空间的容量
  - 造成存储空间的“碎片”

1.2 线性表的存储结构

typedef struct
{
    int data[20]; /* 数组，存储数据元素 */
    int length;             /* 线性表当前长度 */
}SqList;

存储空间的起始位置：数组data它的存储位置就是存储空间的存储位置
线性表的最大存储容量：数组长度20
线性表的当前长度：length

1.3 线性表的创建

/* 初始化顺序线性表 */
int InitList(SqList* l)
{
    l->length = 0;

    return 1;
}

1.4 线性表的整表创建

1.5 线性表的整表删除

1.6 线性表的插入

插入数据的实现过程：

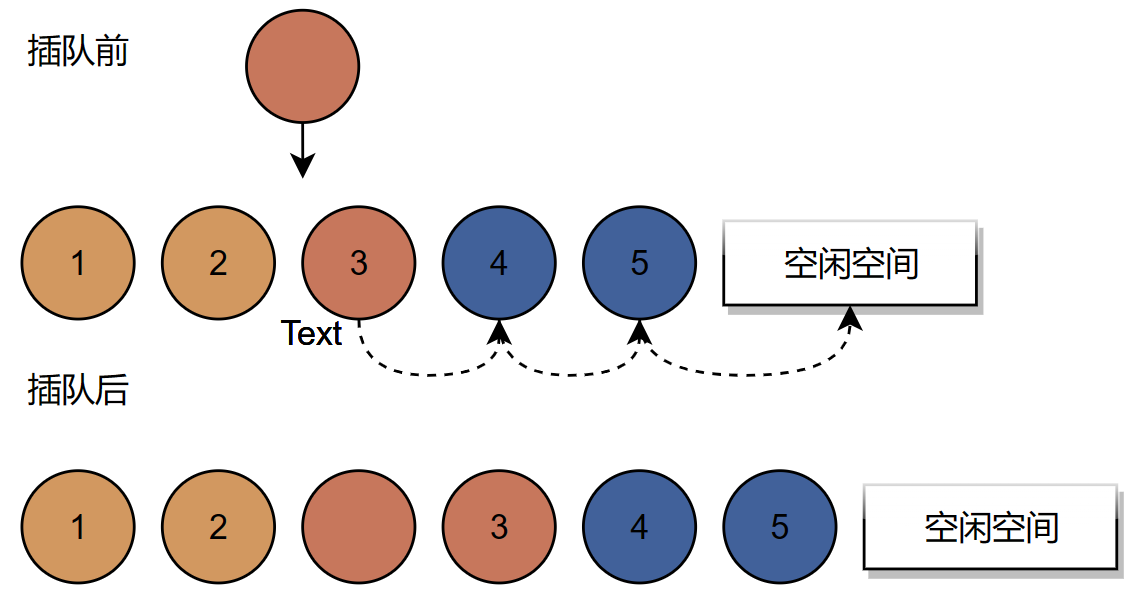
线性表的插入过程

插入算法的思路：

如果插入位置不合理，抛出异常；
如果线性表长度大于等于数组长度，则抛出异常或动态增加容量；
从最后一个元素开始向前遍历到第j个位置，分别将它们都向后移动—个位置；
将要插入元素填入位置j处；
表长加1。

实现代码如下：

///* 初始条件：顺序线性表L已存在,1≤i≤ListLength(L)， */
///* 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 */
int ListInsert(SqList* l, int i, int e)
{
    if (l->length > 20)                /* 顺序线性表已满 */
        return 0;
    if (i < 1 || i > l->length+1)      /* 当i比第一位置小或者比最后一位最后一个位置还要大时 */
        return 0;
    if (i <= l->length)                /* 若插入数据位置不在表尾 */
    {
        for (int j = l->length-1; j >= i-1; j--) /* 将要插入的位置后的元素向后移动一位   length-1和i-1的作用时将真实的位置和数组的位置对应起来 */
        {
            l->data[j + 1] = l->data[j];   
        }
    }
    
    l->data[i-1] = e;                   /* 将新元素插入 */
    l->length++;

    return 1;
}

1.7 线性表的删除

删除数据的实现过程：

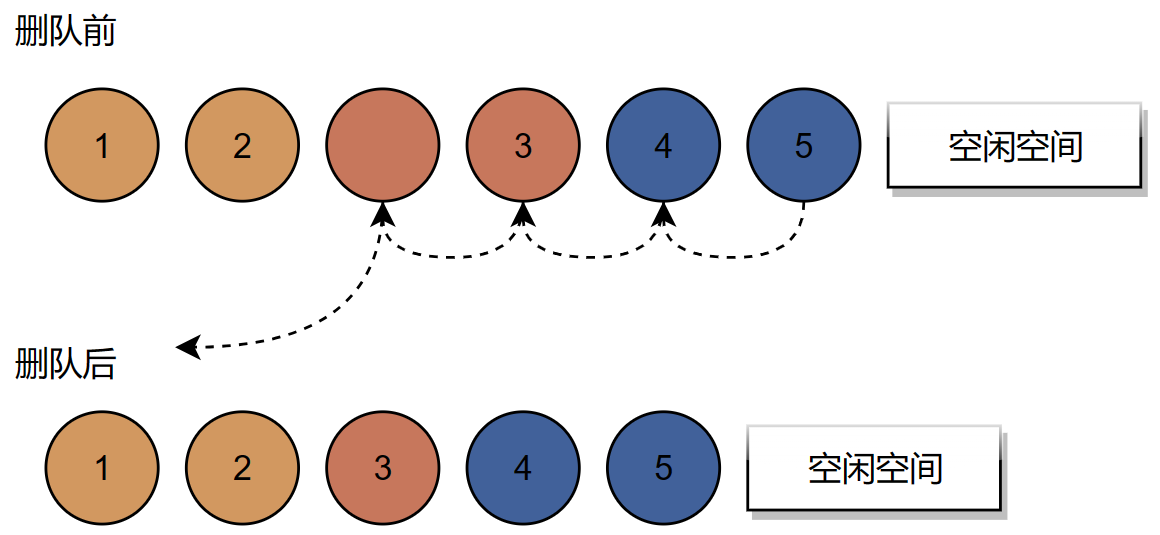
线性表的删除过程

删除算法的思路：

如果删除位置不合理’抛出异常；
取出删除元素；
从删除元素位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置；
表长减1。

实现代码如下:

///* 初始条件：顺序线性表L已存在，1≤i≤ListLength(L) */
///* 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1 */
int ListDelete(SqList* l, int i)
{
    int e = 0;
    if (l->length <= 0)                                 /* 线性表为空 */
        return 0;
    if (i < 1 || i > l->length)                         /* 删除的位置不正确 */
        return 0;
    e = l->data[i - 1];
    if (i < l->length)                                  /* 如果删除的不是最后的位置 */
    {
        for (int j = i - 1; j <= l->length - 1; j++)    /* 将删除的位置后继元素前移 */
        {
            l->data[j] = l->data[j + 1];
        }
    }
    l->length--;

    return e;
}

1.8 线性表的完整代码

#include "stdio.h"  
#include <stdlib.h>

typedef struct
{
    int data[20];           /* 数组，存储数据元素 */
    int length;             /* 线性表当前长度 */
}SqList;

/* 初始化顺序线性表 */
int InitList(SqList* l)
{
    l->length = 0;

    return 1;
}

///* 初始条件：顺序线性表L已存在,1≤i≤ListLength(L)， */
///* 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 */
int ListInsert(SqList* l, int i, int e)
{
    if (l->length > 20)
        return 0;
    if (i < 1 || i > l->length + 1)
        return 0;
    if (i <= l->length)
    {
        for (int j = l->length - 1; j >= i - 1; j--)
        {
            l->data[j + 1] = l->data[j];
        }
    }

    l->data[i - 1] = e;
    l->length++;

    return 1;
}

///* 初始条件：顺序线性表L已存在，1≤i≤ListLength(L) */
///* 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1 */
int ListDelete(SqList* l, int i)
{
    int e = 0;
    if (l->length <= 0)
        return 0;
    if (i < 1 || i > l->length)
        return 0;
    e = l->data[i - 1];
    if (i < l->length)
    {
        for (int j = i - 1; j <= l->length - 1; j++)
        {
            l->data[j] = l->data[j + 1];
        }
    }
    l->length--;

    return e;
}

///* 初始条件：顺序线性表L已存在 */
///* 操作结果：依次对L的每个数据元素输出 */
void ListTraverse(SqList l)
{
    printf("当前线性表个数：%d\r\n", l.length);
    for (int i = 0; i < l.length; i++)
    {
        printf("%d ", l.data[i]);
    }
    printf("\r\n");
}

int main()
{
    SqList L;
    int status = 0;

    InitList(&L);
    for (int i = 0; i < 5; i++)
    {
        status = ListInsert(&L, 1, i);
    }
    status = ListInsert(&L, 2, 6);

    ListTraverse(L);
    status = ListDelete(&L, 2);
    printf("删除的数据：%d\r\n", status);
    ListTraverse(L);
    status = ListInsert(&L, 2, 9);
    ListTraverse(L);

    return 0;
}

2. 单向链表

1.1 单向链表的定义

n个结点（a的存储映像）链结成一个链表，即为线性表的链式存储结构，因为此链表的每个结点中只包含一个指针域，所以叫做单链表。

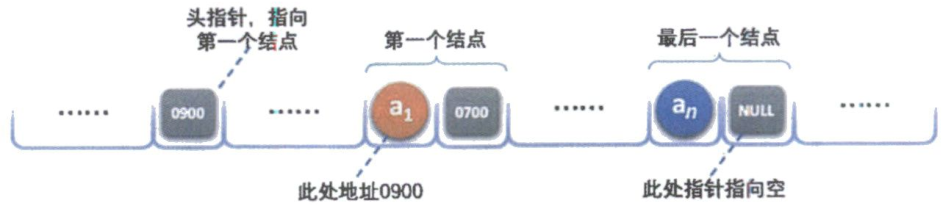
头指针和头结点
- 头指针
  - 头指针是指链表指向第一个结点的指针，若链表有头结点，则是指向头结点的指针；
  - 头指针具有标志作用，所以常用头指针冠以链表的名字；
  - 无论链表是否为空，头指针均不为空。头指针是链表的必要元素。
- 头结点
  - 头结点是为了操作的统一和方便而设立的，放在第一元素的结点之前，其数据域一般无意义（也可存放链表的长度）；
  - 有了头结点，对在第一元素结点前插入结点和删除第一结点，其操作与其他结点的操作就统一了；
  - 头结点不一定是链表必需要素。

1.2 单向链表的存储结构

/* 线性表的单链表存储结构 */
typedef struct Node
{
    int data;
    struct Node * next;
}Node;

线性表的数据存储位置：data
指向下一个链表的结点：struct Node * next

1.3 单向链表的创建

/* 初始化链式线性表 */
int InitList(Node** L)
{
    //Node* L = malloc(sizeof(Node));
    //L->next = NULL; /* 指针域为空 */

    *L = (Node*)malloc(sizeof(Node)); /* 产生头结点,并使L指向此头结点 */
    if (!(*L)) /* 存储分配失败 */
        return 0;
    (*L)->next = NULL; /* 指针域为空 */

    return 1;
}

1.4 单向链表的整表的创建

1.4.1 头插法整表创建

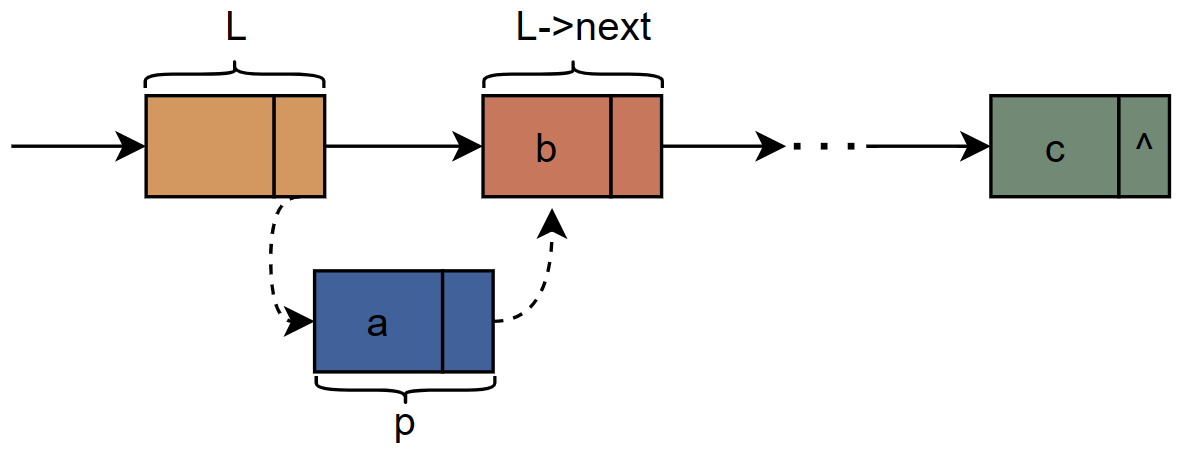
代码实现过程：

void CreateListF(Node** L, int a[], int n)   //头插法输入数据
{
    Node* s;
    *L = malloc(sizeof(Node));
    (*L)->next = NULL;

    for (int i = 0; i < n; i++)
    {
        s = (Node*)malloc(sizeof(Node));
        s->data = a[i];
        s->next = (*L)->next;
        (*L)->next = s;
    }
}

1.4.2 尾插法整表创建

代码实现过程：

void CreateListR(Node** L, int a[], int n)   //尾插法输入数据
{
    Node* s, * p;

    *L = malloc(sizeof(Node));
    p = *L;  //必须的
    for (int i = 0; i < n; i++)
    {
        s = (Node*)malloc(sizeof(Node));
        s->data = a[i];
        p->next = s;
        p = s;
    }
    p->next = NULL;
}

1.5 单向链表的整表删除

单链表整表删除的算法思路如下：

声明一指针p和q；
将第一个结点赋值给p。
循环:
- 将下—结点赋值给q；
- 释放p；
- 将q赋值给p。

实现代码算法如下：

/* 初始条件：链式线性表L已存在。
操作结果：将L重置为空表*/
int ClearList(Node **L)
{
	Node *p, *q;
	p = (*L)->next;
	while(p)
	{
		q = p->next;
		free(p);
		p = q;
	}
	(*L)->next = NULL;
	return 1;
}

1.6 单向链表的插入

单向链表的插入过程：

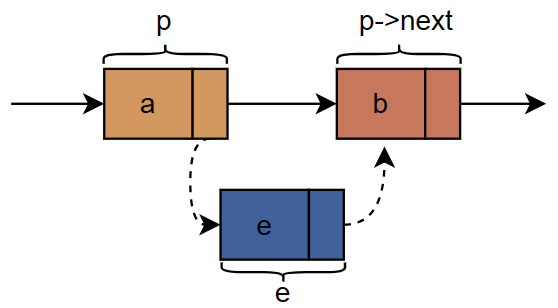
单链表第j个数据插入结点的算法思路：

声明—指针p指向链表头结点’初始化／从l开始;
当j<i时，就遍历链表，让P的指针向后移动，不断指向下—结点，j累加1；
若到链表末尾p为空，则说明第i个结点不存在；
否则查找成功，在系统中生成—个空结点s；
将数据元素e赋值给s->data；
单链表的插入标准语句s-＞next＝p-＞next；p-＞next＝s；
返回成功。

实现代码算法如下:

/* 初始条件：链式线性表L已存在,1≤i≤ListLength(L)， */
/* 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 */
void ListInsert(Node* L, int i, int e)
{
    int j;
    Node *p, *s;
    p = L;
    j = 1;
    while (p && j < i)     /* 寻找第i个结点 */
    {
        p = p->next;
        ++j;
    }
    if (!p || j > i)
        return 0;          /* 第i个元素不存在 */
    s = (Node*)malloc(sizeof(Node));  /*  生成新结点(C语言标准函数) */
    s->data = e;
    s->next = p->next;      /* 将p的后继结点赋值给s的后继  */
    p->next = s;          /* 将s赋值给p的后继 */
}

1.7 单向链表的删除

单向链表的删除过程：

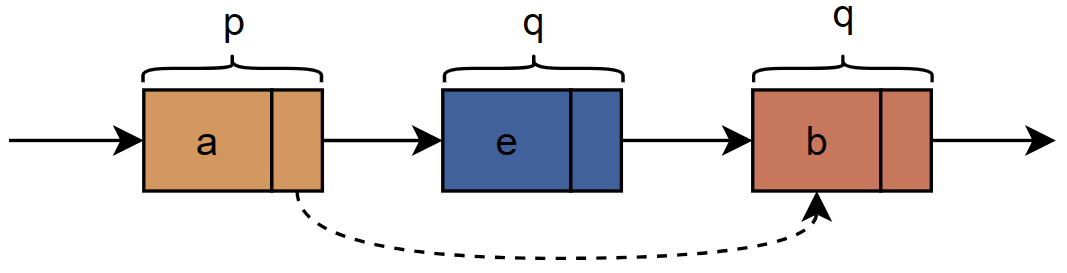
单链表第i个数据删除结点的算法思路：

声明一指针p指向链表头结点，初始化j从1开始；
当j＜i时，就遍历链表，让p的指针向后移动，不断指向下一个结点，j累加1；
若到链表末尾p为空，则说明第i个结点不存在；
否则查找成功，将欲删除的结点p-＞next赋值给q；
单链表的删除标准语句p-＞next＝q-＞next；
将q结点中的数据赋值给e，作为返回；
释放q结点；
返回成功。

实现代码算法如下:

/* 初始条件：链式线性表L已存在,1≤i≤ListLength(L)， */
/* 操作结果：删除一个数据 */
void ListDelect(Node* L, int i)
{
    int j;
    Node* p, * s;
    p = L;
    j = 1;
    while (p && j < i)     /* 寻找第i个结点 */
    {
        p = p->next;
        ++j;
    }
    if (!p || j > i)
        return 0;   /* 第i个元素不存在 */

    s = p->next;
    p->next = s->next;
    free(s);
}

1.8 单向链表的完整代码

#include "stdio.h"  
#include <stdlib.h>

typedef struct Node
{
    int data;
    struct Node * next;
}Node;

/* 初始条件：链式线性表L已存在,1≤i≤ListLength(L)， */
/* 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 */
void ListInsert(Node* L, int i, int e)
{
    int j;
    Node *p, *s;
    p = L;
    j = 1;
    while (p && j < i)     /* 寻找第i个结点 */
    {
        p = p->next;
        ++j;
    }
    if (!p || j > i)
        return 0;   /* 第i个元素不存在 */
    s = (Node*)malloc(sizeof(Node));  /*  生成新结点(C语言标准函数) */
    s->data = e;
    s->next = p->next;      /* 将p的后继结点赋值给s的后继  */
    p->next = s;          /* 将s赋值给p的后继 */
}
/* 初始条件：链式线性表L已存在,1≤i≤ListLength(L)， */
/* 操作结果：删除一个数据 */
void ListDelect(Node* L, int i)
{
    int j;
    Node* p, * s;
    p = L;
    j = 1;
    while (p && j < i)     /* 寻找第i个结点 */
    {
        p = p->next;
        ++j;
    }
    if (!p || j > i)
        return 0;   /* 第i个元素不存在 */

    s = p->next;
    p->next = s->next;
    free(s);
}

void ListTraverse(Node *L)
{
    while (L->next != NULL)
    {
        printf("%d ", L->next->data);
        L = L->next;
    }
    printf("\n");
}

void CreateListF(Node** L, int a[], int n)   //头插法输入数据
{
    Node* s;
    *L = malloc(sizeof(Node));
    (*L)->next = NULL;

    for (int i = 0; i < n; i++)
    {
        s = (Node*)malloc(sizeof(Node));
        s->data = a[i];
        s->next = (*L)->next;
        (*L)->next = s;
    }
}

void CreateListR(Node** L, int a[], int n)   //尾插法输入数据
{
    Node* s, * p;

    *L = malloc(sizeof(Node));
    p = *L;
    for (int i = 0; i < n; i++)
    {
        s = (Node*)malloc(sizeof(Node));
        s->data = a[i];
        p->next = s;
        p = s;
    }
    p->next = NULL;
}

/* 初始化链式线性表 */
int InitList(Node** L)
{
    *L = (Node*)malloc(sizeof(Node)); /* 产生头结点,并使L指向此头结点 */
    if (!(*L)) /* 存储分配失败 */
        return 0;
    (*L)->next = NULL; /* 指针域为空 */

    return 1;
}

int main()
{
    Node* L;
    int a[10] = { 1,2,3,4,5,6,7,8,9,10 };

    InitList(&L);
    CreateListR(&L, a, 10);

    for (int j = 1; j <= 5; j++)
        ListInsert(L, 1, j);
    printf("在L的表头依次插入1～5后：L.data=");
    ListTraverse(L);
    ListDelect(L, 3);
    ListTraverse(L);

    return 0;
}

3. 双向链表

1.1 双向链表的定义

双向链表是在单链表得每个结点中，再设置一个指向其前驱结点得指针域。

1.2 双向链表的存储结构

typedef struct DNode
{
	int data;
	struct DNode* prior;
	struct DNode* next;
}DLinkList;
typedef DLinkList* LinkList;

1.4 双向链表的整表创建

1.4.1 头插法整表创建

void CreateListF(LinkList* L, int a[], int n)    //头插法输入数据
{
	LinkList s;
	*L = (LinkList)malloc(sizeof(LinkList));
	(*L)->prior = NULL;
	(*L)->next = NULL;

	for (int i = 0; i < n; i++)
	{
		s = (LinkList)malloc(sizeof(LinkList));
		s->data = a[i];

		s->prior = *L;
		s->next = (*L)->next;
		(*L)->next = s;
	}
}

1.4.2 尾插法整表创建

void CreateListR(LinkList* L, int a[], int n)     //尾插法输入数据
{
	LinkList s,  p;
	*L = (LinkList)malloc(sizeof(LinkList));
	p = *L;
	for (int i = 0; i < n; i++)
	{
		s = (LinkList)malloc(sizeof(LinkList));
		s->data = a[i];
		p->next = s;
		s->prior = p;
		p = s;
	}
	p->next = NULL;
}

1.5 双向链表的整表删除

1.6 双向链表的插入

双向链表的插入过程：

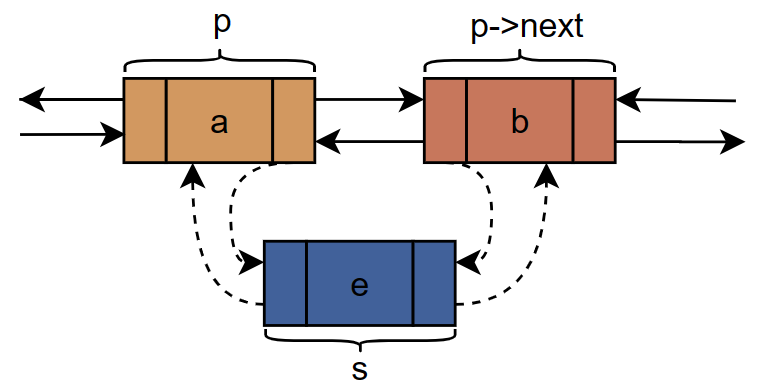
代码实现过程：

int ListInsert(LinkList* L, int n, int e)    //插入数据
{
	LinkList s,  r = *L;
	int j = 0;
	while (j < n - 1 && r != NULL)
	{
		j++;
		r = r->next;
	}
	if (r == NULL)
		return 0;
	else
	{
		s = (LinkList)malloc(sizeof(LinkList));
		s->data = e;
		s->prior = r;
		s->next = r->next;
		r->next->prior = s;
		r->next = s;


		return 1;
	}
}

1.7 双向链表的删除

双向链表的删除过程：

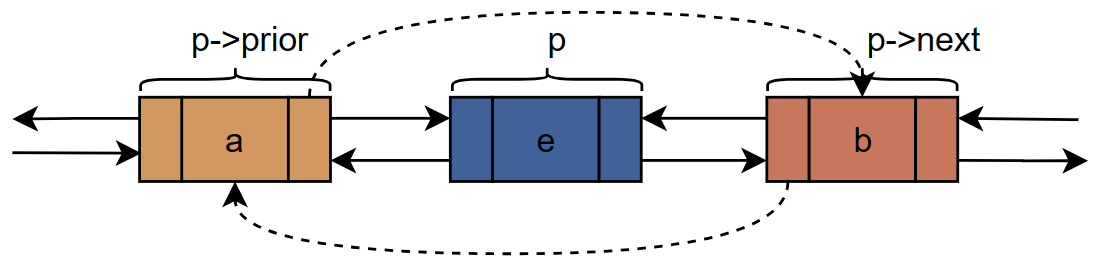
代码实现过程：

int ListDelete(LinkList L, int i, int *e)    //删除数据
{
	int j = 1;
	LinkList s, p;
	p = L;
	while (p && j < i)
	{
		p = p->next;
		j++;
	}
	if (i != j)
		return 0;
	s = p->next;
	*e = s->data;
	p->next = s->next;
	s->next->prior = p;
	free(s);

	return 1;
}

1.8 双向链表的完整代码

#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>

typedef struct DNode
{
	int data;
	struct DNode* prior;
	struct DNode* next;
}DLinkList;
typedef DLinkList* LinkList;

void CreateListF(LinkList* L, int a[], int n)    //头插法输入数据
{
	LinkList s;
	*L = (LinkList)malloc(sizeof(LinkList));
	(*L)->prior = NULL;
	(*L)->next = NULL;

	for (int i = 0; i < n; i++)
	{
		s = (LinkList)malloc(sizeof(LinkList));
		s->data = a[i];

		s->prior = *L;
		s->next = (*L)->next;
		(*L)->next = s;
	}
}

void CreateListR(LinkList* L, int a[], int n)     //尾插法输入数据
{
	LinkList s,  p;
	*L = (LinkList)malloc(sizeof(LinkList));
	p = *L;
	for (int i = 0; i < n; i++)
	{
		s = (LinkList)malloc(sizeof(LinkList));
		s->data = a[i];
		p->next = s;
		s->prior = p;
		p = s;
	}
	p->next = NULL;
}

int ListInsert(LinkList* L, int n, int e)    //插入数据
{
	LinkList s,  r = *L;
	int j = 0;
	while (j < n - 1 && r != NULL)
	{
		j++;
		r = r->next;
	}
	if (r == NULL)
		return 0;
	else
	{
		s = (LinkList)malloc(sizeof(LinkList));
		s->data = e;
		s->prior = r;
		s->next = r->next;
		r->next->prior = s;
		r->next = s;


		return 1;
	}
}

// int ListDelete(DLinkList* L, int n)    //删除数据

void DispList(LinkList L)      //输出数据
{
	while (L->next != NULL)
	{
		printf("%d ", L->next->data);
		L = L->next;
	}
	printf("\n");
}

int main()
{
	LinkList L;
	int a[] = { 1,2,3,4,5,6,7,8,9,10 };
	CreateListR(&L, a, 10);    //头插法输入数据
	DispList(L);
	ListInsert(&L, 4, 9);   //插入数据
	DispList(L);

	return 0;
}

4. 顺序栈

4.1 顺序栈的定义

栈（Stack）是限定仅在表尾进行插入和删除操作的线性表。

把允许插入和删除的一端称为栈顶（top），另一端称为栈底（bottom），不含任何数据元素的栈称为空栈。栈又称为后进先出的线性表。

4.2 顺序栈的存储结构

/* 顺序栈结构 */
typedef struct
{
    int data[20];
    int top; /* 用于栈顶指针 */
}SqStack;

4.3 顺序栈的创建

/*  构造一个空栈S */
int InitStack(SqStack* s)
{
    s->top = -1;

    return 1;
}

4.4 顺序栈的插入

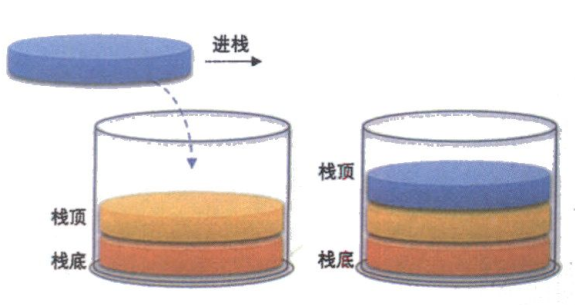
顺序栈数据入栈的算法思路：

判断顺序栈是否是满栈；
如果不是满栈，将栈顶指针加一；
将新数据插入到栈顶；
返回成功。

实现代码算法如下:

/* 插入元素e为新的栈顶元素 */
int Push(SqStack* s, int e)
{
    if (s->top == 20 - 1)
        return 0;
    s->top++;
    s->data[s->top] = e;

    return 1;
}

4.5 顺序栈的删除

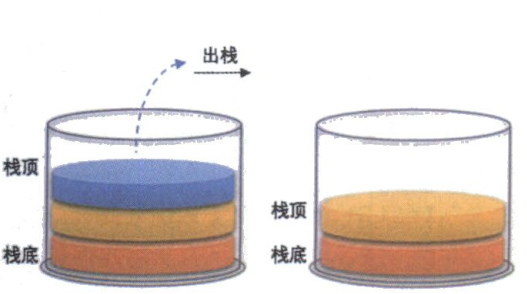
顺序栈数据出栈的算法思路：

判断顺序栈是否是空栈；
如果不是空栈，把要删除得栈顶数据返回，同时将栈顶指针加一；
返回成功。

实现代码算法如下:

/* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */
int Pop(SqStack* s, int *data)
{
    if (s->top == -1)
        return 0;
    *data = s->data[s->top];
    s->top--;

    return 1;
}

4.6 顺序栈的完整代码

#include "stdio.h"  
#include "stdlib.h"   

/* 顺序栈结构 */
typedef struct
{
    int data[20];
    int top; /* 用于栈顶指针 */
}SqStack;

/*  构造一个空栈S */
int InitStack(SqStack* s)
{
    s->top = -1;

    return 1;
}
//
///* 若栈不空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR */
//GetTop
//
/* 插入元素e为新的栈顶元素 */
int Push(SqStack* s, int e)
{
    if (s->top == 20 - 1)
        return 0;
    s->top++;
    s->data[s->top] = e;

    return 1;
}

/* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */
int Pop(SqStack* s, int *data)
{
    if (s->top == -1)
        return 0;
    *data = s->data[s->top];
    s->top--;

    return 1;
}

/* 从栈底到栈顶依次对栈中每个元素显示 */
int StackTraverse(SqStack s)
{
    int i;
    i = 0;
    while (i <= s.top)
    {
        printf("%d ", s.data[i++]);
    }
    printf("\n");
    return 1;
}

int main()
{
    int data;
    SqStack s;

    InitStack(&s);
    Push(&s, 5);
    Push(&s, 3);
    Push(&s, 8);
    StackTraverse(s);
    Pop(&s, &data);
    printf("%d\r\n", data);
    StackTraverse(s);
    return 0;
}

5. 两栈共享空间

6. 链式栈

4.1 链式栈的定义

链式队列，简称"链队列"，即使用链表实现的队列存储结构。

链式队列的实现思想同顺序队列类似，只需创建两个指针（命名为 top 和 rear）分别指向链表中队列的队头元素和队尾元素。

4.2 链式栈的存储结构

typedef struct StackNode
{
	int data;
	struct StackNode* next;
}StackNode, * LinkStackPtr;

typedef struct LinkStack
{
	LinkStackPtr top;
	int count;
}LinkStack;

4.3 链式栈的创建

/*  构造一个空栈S */
int InitStack(LinkStack* s)
{
    s->top = (LinkStackPtr*)malloc(sizeof(StackNode));
    s->top->next = NULL;
    s->count = 0;

    return 1;
}

4.4 链式栈的插入

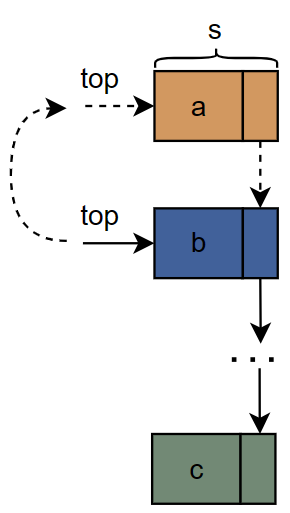
链式栈数据入栈的算法思路：

声明一个新的结点，并将要插入的数据赋值放入结点中；
将结点指向栈中栈顶元素；
将新的结点赋值给栈顶指针；
栈的元素计数加一；
返回成功。

实现代码算法如下:

/* 插入元素e为新的栈顶元素 */
int Push(LinkStack* s, int e)
{
    LinkStackPtr p = (LinkStackPtr)malloc(sizeof(StackNode));
    p->data = e;
    p->next = s->top;
    s->top = p;
    s->count++;

    return 1;
}

4.5 链式栈的删除

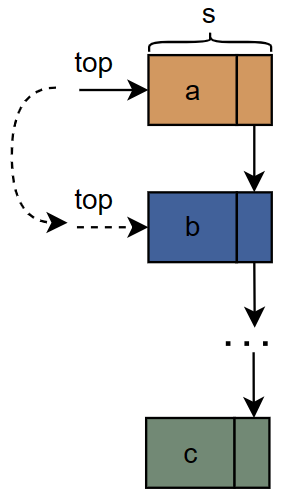
链式栈数据出栈的算法思路：

声明一个新的结点；
判断当前栈是否为空；
把要删除的结点保存的数据返回；
把栈顶结点赋值给新的结点；
把栈顶指针向下移动一位；
释放新结点也就是栈顶元素；
栈的元素计数减一；
返回成功。

实现代码算法如下:

/* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */
int Pop(LinkStack* s, int *e)
{
    LinkStackPtr p;
    p = s->top;
    *e = p->data;
    s->top = s->top->next;
    free(p);
    s->count--;

    return 1;
}

4.6 链式栈的完整代码

#include "stdio.h"
#include "malloc.h"
#include <stdlib.h>

typedef struct StackNode
{
	int data;
	struct StackNode* next;
}StackNode, * LinkStackPtr;

typedef struct LinkStack
{
	LinkStackPtr top;
	int count;
}LinkStack;


/*  构造一个空栈S */
int InitStack(LinkStack* s)
{
    s->top = (LinkStackPtr*)malloc(sizeof(StackNode));
    s->top->next = NULL;
    s->count = 0;

    return 1;
}

/* 插入元素e为新的栈顶元素 */
int Push(LinkStack* s, int e)
{
    LinkStackPtr p = (LinkStackPtr)malloc(sizeof(StackNode));
    p->data = e;
    p->next = s->top;
    s->top = p;
    s->count++;

    return 1;
}

/* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */
int Pop(LinkStack* s, int *e)
{
    LinkStackPtr p;
    p = s->top;
    *e = p->data;
    s->top = s->top->next;
    free(p);
    s->count--;

    return 1;
}

int StackTraverse(LinkStack S)
{
    LinkStackPtr p;
    p = S.top;
    while (p)
    {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
    return 1;
}

int main()
{
    int e = 0;
    LinkStack s;

    InitStack(&s);
    for(int i = 0; i < 10; i++)
        Push(&s, i);
    StackTraverse(s);
    Pop(&s, &e);
    printf("%d\r\n", e);
    StackTraverse(s);

    Pop(&s, &e);
    printf("%d\r\n", e);
    StackTraverse(s);

    return 0;
}

4.7 链式栈的应用 --- 四则运算表达式

4.7.1 定义

波兰表示法（Polish notation，或波兰记法），是一种逻辑、算术和代数表示方法，其特点是操作符置于操作数的前面，因此也称做前缀

表示法。如果操作符的元数是固定的，则语法上不需要括号仍然能被无歧义地解析。

波兰表达式也称为前缀表达式，逆波兰表达式也称为后缀表达式。以表达式 (1 + 2) * (3 + 4) 为例，这个表达式称为中缀表达式。

表达式	描述	结果
前缀表达式	不含括号的的算数表达式，将运算符写在前面，操作数写在后面	* + 1 2 + 3 4
中缀表达式	必须含括号，操作符处于操作数的中间	( 1 + 2 ) * ( 3 + 4 )
后缀表达式	不含括号，运算符放在两个运算对象的后面。	1 2 + 3 4 + *

与中缀表达式相比，前缀表达式和后缀表达式有个好处，没有圆括号，在计算的时候无需考虑优先级，能够提高计算机的运算效率。

4.7.2 中缀表达式转后缀表达式

视频展示

转换过程：

从左至右依次遍历中缀表达式各个字符（需要准备一个字符栈存储操作符和括号）

字符为 运算数 ：

直接送入后缀表达式（注：需要先分析出完整的运算数）。
字符为 **左括号 **：

直接入栈（注：左括号入栈后优先级降至最低）。
字符为 右括号 ：

直接出栈，并将出栈字符依次送入后缀表达式，直到栈顶字符为左括号（左括号也要出栈，但不送入后缀表达式）。

总结：只要满足栈顶为左括号即可进行最后一次出栈。

字符为 操作符 ：

若栈空，直接入栈。

若栈非空，判断栈顶操作符，若栈顶操作符优先级低于该操作符，该操作符入栈；否则一直出栈，并将出栈字符依次送入后缀表达式，直到栈空或栈顶操作符优先级低于该操作符，该操作符再入栈。

总结：只要满足栈空或者优先级高于栈顶操作符即可停止出栈，并将该操作符入栈。

重复以上步骤直至遍历完成中缀表达式，接着判断字符栈是否为空，非空则直接出栈，并将出栈字符依次送入后缀表达式。

注：中缀表达式遍历完成，栈中可能还有字符未输出，故需要判断栈空。

算法展示：

void InfixToPostfix(char *infix, char *postfix)// 将中缀表达式转为后缀表达式
{
    Stack L;
    char* p, *q;
    p = infix;
    q = postfix;
    int priority = 0;
    int priority_top = 0;

    InitStack(&L);                 //初始化栈
    while (*p != '\0')             //遍历输入的数据
    {
        if (isNumber(*p))          //检查当前数据是否为数字
        {
            while (isNumber(*p) || (*p == '.'))  //如果是数字或者小数点，继续读取下一个
            {
                *q = *p;
                q++;
                p++;
            }
            *q = ' ';// 输出空格，用来将每组数字和运算分隔开
            q++;
        }
        else
        {
            if (isOperator(*p))     //如果是运算符
            {
                priority = GetPriority(*p);    //获取当前运算符的运算优先级
                while(!isEmpty(&L))            //如果栈为空，则把运算符入栈
                {
                    priority_top = GetPriority(Top(&L));   //获取栈顶元素
                    if (priority <= priority_top)          //如果栈顶元素的优先级大于或者等于当前运算符的优先级
                    {
                        *q = Pop(&L);                     //把栈顶元素出栈
                        q++;
                        *q = ' ';// 输出空格
                        q++;
                    }
                    else
                        break;                           //如果小于优先级则结束，把当前运算符入栈
                }
                Push(&L, *p);
            }
            else if (*p == ')')                          //如果是右括号
            {
                while (Top(&L) != '(')              //把左右括号之间的所有元素出栈
                {
                    *q = Pop(&L);
                    q++;
                    *q = ' ';// 输出空格
                    q++;
                }
                *q = Pop(&L);
            }
            else                                   //如果是左括号则入栈
                Push(&L, *p);
            p++;
        }
    }
    while (!isEmpty(&L))                              //把栈中剩余的运算符全部出栈
    {
        *q = Pop(&L);
        q++;
        *q = ' ';// 输出空格
        q++;
    }
    *q = '\0';
}

4.7.3 计算后缀表达式的值

视频展示

计算过程：

从左至右依次遍历后缀表达式各个字符（需要准备一个运算数栈存储运算数和操作结果）

字符为运算数：

直接入栈（注：需要先分析出完整的运算数并将其转换为对应的数据类型）
字符为 操作符 ：

连续出栈两次，使用出栈的两个数据进行相应计算，并将计算结果入栈

注意：第一个出栈的运算数为 a ，第二个出栈的运算数为 b ，此时的操作符为 - ，则计算 b-a（注：a和b顺序不能反），并将结果入栈。

重复以上步骤直至遍历完成后缀表达式，最后栈中的数据就是中缀表达式的计算结果。

算法展示：

double Evaluate(char* postfix)            // 计算后缀表达式的值
{
    Stack L;
    char str[50] = { 0 };
    char* p, * q;
    p = postfix;
    q = str;

    InitStack(&L);                     //初始化栈
    while (*p != '\0')
    {
        if (isNumber(*p))              //如果当前元素是数字
        {
            *q = *p;                   //保存这个数字
            q++;
            p++;
            if (*p != ' ')            //判断下一个元素是否为空格，如果不是空格则说明数字是多位的
            {
                while (*p != ' ')     //循环获取数字，直到空格
                {
                    *q = *p;
                    q++;
                    p++;
                }
            }
            Push(&L, atof(str));                //将获取到的多位字符型数字转换为数字并入栈
            memset(str, 0, sizeof(char) * 50);  //清空数组
            q = str;                            //把指针重新指向数组起始位置
        }
        else                         //如果当前元素是运算符
        {
            double priority1 = Pop(&L);      //取出栈顶元素
            double priority2 = Pop(&L);      //取出栈顶元素
            double result = Operate(priority1, priority2, *p);   //将取出的两个栈顶元素做运算
            printf("四则运算：%g %c %g = %g\r\n", priority2, *p, priority1, result);
            Push(&L, result);                //将运算结果入栈
        }
        p++;
        while(*p == ' ')                    //如果当前元素是空格，则继续指向下一个
            p++;
    }
    return Pop(&L);                        //返回栈顶元素即为运算的结果
}

4.7.4 四则运算表达式完整代码


#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>

typedef struct 
{
    double data[100];  // 数组指针
    int top;  // 栈顶指针
} Stack;

int InitStack(Stack* s)
{
    s->top = -1;

    return 1;
}

int Push(Stack* s, double e)
{
    if (s->top == 100 - 1)
    {
        printf("Push Stack overflow\n");
        exit(1); // 若栈为满，则退出程序
    }
    s->top++;
    s->data[s->top] = e;

    return 1;
}

double Pop(Stack* s)
{
    if (s->top == -1)
    {
        printf("Pop Stack underflow\n");
        exit(1); // 若栈为空，则退出程序
    }
    double e = s->data[s->top];
    s->top--;

    return e;
}

/* 从栈底到栈顶依次对栈中每个元素显示 */
int StackTraverse(Stack s)
{
    int i;
    i = 0;
    while (i <= s.top)
    {
        printf("StackTraverse: %c ", s.data[i++]);
    }
    printf("\n");
    return 1;
}

// 判断栈是否为空
int isEmpty(Stack* s) {
    return s->top == -1;
}

// 获取栈顶元素
double Top(Stack* s) {
    if (isEmpty(s)) { // 检查栈是否为空
        printf("Stack underflow\n");
        exit(1); // 若栈为空，则退出程序
    }

    return s->data[s->top]; // 返回栈顶元素的值
}

int isNumber(char c)
{
    if (c >= '0' && c <= '9')
    {
        return 1;   //为数字
    }
    else
        return 0;   //为符号
}

int GetPriority(char c)// 获取当前运算符的优先级
{
    switch(c) 
    {
        case '+': return 1;
        case '-': return 1;
        case '*': return 2;
        case '/': return 2;
        default: return 0;
    }
}

// 判断是否为运算符
int isOperator(char c) 
{
    return c == '+' || c == '-' || c == '*' || c == '/';
}

// 四则运算
double Operate(double num1, double num2, char c)
{
    switch (c)
    {
        case '+': return num2 + num1;
        case '-': return num2 - num1;
        case '*': return num2 * num1;
        case '/': return num2 / num1;
    }
}

void InfixToPostfix(char *infix, char *postfix)// 将中缀表达式转为后缀表达式
{
    Stack L;
    char* p, *q;
    p = infix;
    q = postfix;
    int priority = 0;
    int priority_top = 0;

    InitStack(&L);                 //初始化栈
    while (*p != '\0')             //遍历输入的数据
    {
        if (isNumber(*p))          //检查当前数据是否为数字
        {
            while (isNumber(*p) || (*p == '.'))  //如果是数字或者小数点，继续读取下一个
            {
                *q = *p;
                q++;
                p++;
            }
            *q = ' ';// 输出空格，用来将每组数字和运算分隔开
            q++;
        }
        else
        {
            if (isOperator(*p))     //如果是运算符
            {
                priority = GetPriority(*p);    //获取当前运算符的运算优先级
                while(!isEmpty(&L))            //如果栈为空，则把运算符入栈
                {
                    priority_top = GetPriority(Top(&L));   //获取栈顶元素
                    if (priority <= priority_top)          //如果栈顶元素的优先级大于或者等于当前运算符的优先级
                    {
                        *q = Pop(&L);                     //把栈顶元素出栈
                        q++;
                        *q = ' ';// 输出空格
                        q++;
                    }
                    else
                        break;                           //如果小于优先级则结束，把当前运算符入栈
                }
                Push(&L, *p);
            }
            else if (*p == ')')                          //如果是右括号
            {
                while (Top(&L) != '(')              //把左右括号之间的所有元素出栈
                {
                    *q = Pop(&L);
                    q++;
                    *q = ' ';// 输出空格
                    q++;
                }
                *q = Pop(&L);
            }
            else                                   //如果是左括号则入栈
                Push(&L, *p);
            p++;
        }
    }
    while (!isEmpty(&L))                              //把栈中剩余的运算符全部出栈
    {
        *q = Pop(&L);
        q++;
        *q = ' ';// 输出空格
        q++;
    }
    *q = '\0';
}

double Evaluate(char* postfix)            // 计算后缀表达式的值
{
    Stack L;
    char str[50] = { 0 };
    char* p, * q;
    p = postfix;
    q = str;

    InitStack(&L);                     //初始化栈
    while (*p != '\0')
    {
        if (isNumber(*p))              //如果当前元素是数字
        {
            *q = *p;                   //保存这个数字
            q++;
            p++;
            if (*p != ' ')            //判断下一个元素是否为空格，如果不是空格则说明数字是多位的
            {
                while (*p != ' ')     //循环获取数字，直到空格
                {
                    *q = *p;
                    q++;
                    p++;
                }
            }
            Push(&L, atof(str));                //将获取到的多位字符型数字转换为数字并入栈
            memset(str, 0, sizeof(char) * 50);  //清空数组
            q = str;                            //把指针重新指向数组起始位置
        }
        else                         //如果当前元素是运算符
        {
            double priority1 = Pop(&L);      //取出栈顶元素
            double priority2 = Pop(&L);      //取出栈顶元素
            double result = Operate(priority1, priority2, *p);   //将取出的两个栈顶元素做运算
            printf("四则运算：%g %c %g = %g\r\n", priority2, *p, priority1, result);
            Push(&L, result);                //将运算结果入栈
        }
        p++;
        while(*p == ' ')                    //如果当前元素是空格，则继续指向下一个
            p++;
    }
    return Pop(&L);                        //返回栈顶元素即为运算的结果
}


int main() 
{
    Stack L;
    char infix[100];
    char postfix[100];

    printf("请输入需要运算的表达式: ");
    scanf("%s", infix);

    InfixToPostfix(infix, postfix);// 将中缀表达式转为后缀表达式
    printf("后缀表达式: %s\n\n", postfix);
  
    double result = Evaluate(postfix);// 计算后缀表达式的值
    printf("\n最终结果: %g\n", result);

    return 0;
}

7. 循环顺序队列

7.1 循环顺序队列的定义

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出的线性表。允许插入的一端称为队尾，允许删除的一端称为队头。

把队列的这种头尾相接的顺序存储结构称为循环队列。

列满的条件尾 (rear + 1)％QueueSize = front

因此通用的计算队列长度的公式为:
(rear - front＋QueueSize)％QueueSize

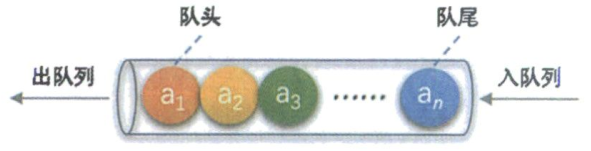
7.2 循环顺序队列的存储结构

/* 循环队列的顺序存储结构 */
typedef struct
{
	int data[20];
	int front;    	/* 头指针 */
	int rear;		/* 尾指针，若队列不空，指向队列尾元素的下一个位置 */
}SqQueue;

7.3 循环顺序队列的创建

/* 初始化一个空队列Q */
int InitQueue(SqQueue* L)
{
	L->front = 0;
	L->rear = 0;

	return 1;
}

7.4 循环顺序队列的插入

循环顺序队列的插入过程：

循环顺序队列的入队的算法实现思路：

判断顺序队列是否是满队列；
把数据放入队尾；
将队尾加一向后移动一位，如果是最后一位了，则移到队头；
返回成功。

实现代码的算法如下：

/* 若队列未满，则插入元素e为Q新的队尾元素 */
int EnQueue(SqQueue* L, int e)
{
	if ((L->rear + 1) % MAXSIZE == L->front)	/* 队列满的判断 */
		return 0;
	L->data[L->rear] = e;
	L->rear = (L->rear + 1) % MAXSIZE;

	return 1;
}

7.5 循环顺序队列的删除

循环顺序队列的删除过程：

循环顺序队列的入队的算法实现思路：

判断顺序队列是否是空队列
取出队列中的数据
将队头加一向后移动一位，如果是最后一位了，则移到队头
返回成功

实现代码的算法如下：

/* 若队列不空，则删除Q中队头元素，用e返回其值 */
int DeQueue(SqQueue* L, int* e)
{
	if (L->front == L->rear)
		return 0;
	*e = L->data[L->front];
	L->front = (L->front + 1) % MAXSIZE;

	return 1;
}

7.6 循环顺序队列的完整代码

#include "stdio.h"
#include "stdlib.h"

#define MAXSIZE 20

/* 循环队列的顺序存储结构 */
typedef struct
{
	int data[MAXSIZE];
	int front;    	/* 头指针 */
	int rear;		/* 尾指针，若队列不空，指向队列尾元素的下一个位置 */
}SqQueue;

/* 初始化一个空队列Q */
int InitQueue(SqQueue* L)
{
	L->front = 0;
	L->rear = 0;

	return 1;
}


/* 若队列未满，则插入元素e为Q新的队尾元素 */
int EnQueue(SqQueue* L, int e)
{
	if ((L->rear + 1) % MAXSIZE == L->front)	/* 队列满的判断 */
		return 0;
	L->data[L->rear] = e;
	L->rear = (L->rear + 1) % MAXSIZE;

	return 1;
}

/* 若队列不空，则删除Q中队头元素，用e返回其值 */
int DeQueue(SqQueue* L, int* e)
{
	if (L->front == L->rear)
		return 0;
	*e = L->data[L->front];
	L->front = (L->front + 1) % MAXSIZE;

	return 1;
}

/* 从队头到队尾依次对队列Q中每个元素输出 */
int QueueTraverse(SqQueue Q)
{
	int i;
	i = Q.front;
	while (i != Q.rear)
	{
		printf("%d ", Q.data[i]);
		i = (i + 1) % MAXSIZE;
	}
	printf("\r\n");
	return 1;
}

int main()
{
	int e;
	SqQueue L;

	InitQueue(&L);

	for (int i = 0; i < 10; i++)
	{
		EnQueue(&L, i);
	}
	QueueTraverse(L);
	DeQueue(&L, &e);
	printf("%d\r\n", e);
	QueueTraverse(L);

	return 0;
}

8.链式队列

8.1 链式队列的定义

队列的链式存储结构，其实就是线性表的单链表，只不过它只能尾进头出而已，简称为链队列。

链式队列一般是有头结点的队列。

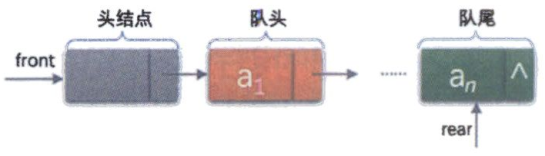
8.2 链式队列的存储结构

typedef struct QNode	/* 结点结构 */
{
	int data;
	struct QNode* next;
}QNode, * QueuePtr;

typedef struct			/* 队列的链表结构 */
{
	QueuePtr front, rear; /* 队头、队尾指针 */
}LinkQueue;

8.3 链式队列的创建

为链式队列申请内存，即为队首指针和队尾指针申请内存。
为链式队列头结点申请内存，头结点不存放有效数据，方便队列的操作。
将队首指针和队尾指针指向头结点，即队首指针和队尾指针相等。
链式队列头结点指针域为空，即为NULL；头结点数据域可不管，亦可为零，作为链式队列有效的节点数，亦可作为创建队列成功标识等等，由开发者根据实际情况而定。

/* 构造一个空队列Q */
int InitQueue(LinkQueue* L)
{
	L->front = L->rear = (QueuePtr)malloc(sizeof(QNode));
	L->front->next = L->rear->next = NULL;


	return 1;
}

8.4 链式队列的插入

链式队列的插入过程：

循环顺序队列的入队的算法实现思路：

为链式队列入队数据结点申请内存。
将新结点设置为最后个结点，新结点的指针域为空，数据域为入队数据。
更新队尾指针，将队尾指针指向新插入的结点。

实现代码的算法如下：

/* 插入元素e为Q的新的队尾元素 */
int EnQueue(LinkQueue* L, int e)
{
	QueuePtr s;

	s = (QueuePtr)malloc(sizeof(QNode));
	s->data = e;
	s->next = NULL;
	L->rear->next = s;
	L->rear = s;

	return 1;
}

8.5 链式队列的删除

链式队列的插入过程：

循环顺序队列的入队的算法实现思路：

只有在链式队列非空时出队数据才有效。
若只有一个有效结点时，需将队尾指针指向头结点，头结点指针域为空。
头结点指针指向下下个有效结点。
结点数据出队。
释放出队结点数据内存。

实现代码的算法如下：

/* 若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR */
int DeQueue(LinkQueue* L, int* e)
{
	QueuePtr s;
	if (L->front == L->rear)
		return 0;
	s = L->front->next;
	*e = s->data;
	L->front->next = s->next;
	if (L->rear == s)
	{
		L->rear = L->front;
	}
	free(s);

	return 1;
}

8.6 链式队列的完整代码

#include "stdio.h"  
#include "stdlib.h"   

typedef struct QNode	/* 结点结构 */
{
	int data;
	struct QNode* next;
}QNode, * QueuePtr;

typedef struct			/* 队列的链表结构 */
{
	QueuePtr front, rear; /* 队头、队尾指针 */
}LinkQueue;

/* 构造一个空队列Q */
int InitQueue(LinkQueue* L)
{
	L->front = L->rear = (QueuePtr)malloc(sizeof(QNode));
	L->front->next = L->rear->next = NULL;


	return 1;
}

/* 若队列不空,则用e返回Q的队头元素,并返回OK,否则返回ERROR */
int GetHead(LinkQueue* L, int* e)
{
	if (L->front == L->rear)
		return 0;
	*e = L->front->next->data;

	return 1;
}

/* 插入元素e为Q的新的队尾元素 */
int EnQueue(LinkQueue* L, int e)
{
	QueuePtr s;

	s = (QueuePtr)malloc(sizeof(QNode));
	s->data = e;
	s->next = NULL;
	L->rear->next = s;
	L->rear = s;

	return 1;
}

/* 若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR */
int DeQueue(LinkQueue* L, int* e)
{
	QueuePtr s;
	if (L->front == L->rear)
		return 0;
	s = L->front->next;
	*e = s->data;
	L->front->next = s->next;
	if (L->rear == s)
	{
		L->rear = L->front;
	}
	free(s);

	return 1;
}

/* 从队头到队尾依次对队列Q中每个元素输出 */
int QueueTraverse(LinkQueue Q)
{
	QueuePtr p;
	p = Q.front->next;
	while (p)
	{
		printf("%d ", p->data);
		p = p->next;
	}
	printf("\r\n");

	return 1;
}

int main()
{
	int e;
	LinkQueue L;
	InitQueue(&L);
	for (int i = 0; i < 10; i++)
	{
		EnQueue(&L, i);
	}
	QueueTraverse(L);
	GetHead(&L, &e);
	printf("头数据：%d\r\n", e);
	DeQueue(&L, &e);
	DeQueue(&L, &e);

	printf("%d\r\n", e);
	QueueTraverse(L);
	GetHead(&L, &e);
	printf("头数据：%d\r\n", e);

	return 0;
}

9. 树

9.1 树的定义

树是n(n≥0)个结点的有限集合，当n=0时，称为空树，这是一个特殊的情况。在任意一棵非空树中应满足：

有且仅有一个特定的称为根的结点
当n>1时，其余结点可分为m(m>0)个互不相交的有限集合，其中每个集合本身又是一棵树，并且称为根节点的子树。

结点的层次（深度）——从上往下数

结点的高度——从下往上数

树的高度——总共多少层

结点的度——有几个孩子

树的度——各结点的度的最大值

9.2 二叉树

9.2.1 二叉树的定义

二叉树：n（n≥0）个结点的有限集合：

或者为空二叉树，即n = 0。
或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。

特点：

每个结点至多只有两棵子树
左右子树不能颠倒（二叉树是有序树)

满二叉树：一颗高度为h，且含有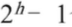个结点的二叉树。

特点：
①只有最后一层有叶子结点

②不存在度为1的结点

③按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1;结点i的父

节点为[i/2]（如果有的话)

完全二叉树：当且仅当其每个结点都与高度为h的满二叉树中编号为1～n的结点一一对应时，称为完全二叉树

特点：

只有最后两层可能有叶子结点
最多只有一个度为1的结点
同左③
i≤[n/2]为分支结点，i>[n/2]为叶子结点

平衡二叉树：树上任一结点的左子树和右子树的深度之差不超过1。

9.2.2 二叉树的存储结构

typedef struct BiTNode  /* 结点结构 */
{
	char data;		/* 结点数据 */
	struct BiTNode* lchild, * rchild; /* 左右孩子指针 */
}BiTNode, * BiTree;

9.2.3 二叉树的建立

要在内存中建立—个二叉树，为了能让每个结点确认是否有左右孩子，我们对它进行了扩展，也就是将二叉树中每个结点的空指针引出一个虚结点，其值为一特定值，比如“＃’’。我们称这种处理后的二叉树为原二叉树的扩展二叉树。扩展二叉树就可以做到一个遍历序列确定—棵二叉树了。

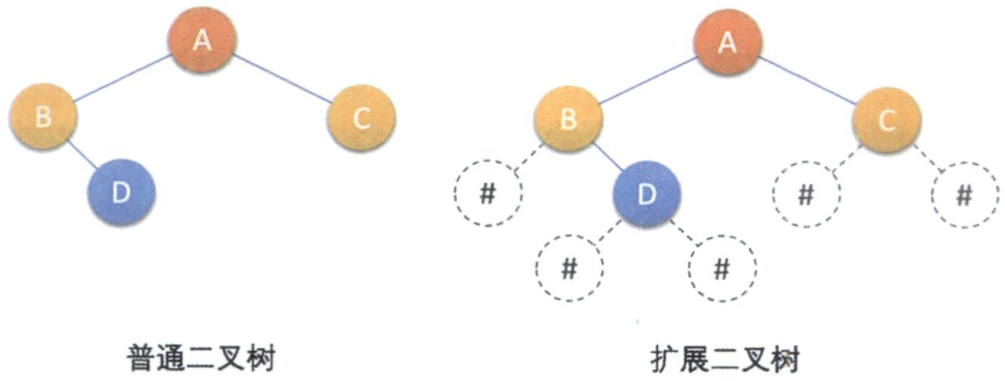
实现代码：

typedef char String[24]; /*  0号单元存放串的长度 */
String str;

Status StrAssign(String T,char *chars)
{ 
	int i;
	if(strlen(chars)>MAXSIZE)
		return ERROR;
	else
	{
		T[0]=strlen(chars);
		for(i=1;i<=T[0];i++)
			T[i]=*(chars+i-1);
		return OK;
	}
}

/* 按前序输入二叉树中结点的值（一个字符） */
/* #表示空树，构造二叉链表表示二叉树T。 */
void CreateBiTree(BiTree *T)
{ 
	TElemType ch;

	/* scanf("%c",&ch); */
	ch=str[treeIndex++];

	if(ch=='#') 
		*T=NULL;
	else
	{
		*T=(BiTree)malloc(sizeof(BiTNode));
		if(!*T)
			exit(OVERFLOW);
		(*T)->data=ch; /* 生成根结点 */
		CreateBiTree(&(*T)->lchild); /* 构造左子树 */
		CreateBiTree(&(*T)->rchild); /* 构造右子树 */
	}
}

StrAssign(str,"ABDH#K###E##CFI###G#J##");

9.2.3 二叉树的先序遍历

先序遍历规则：根左右

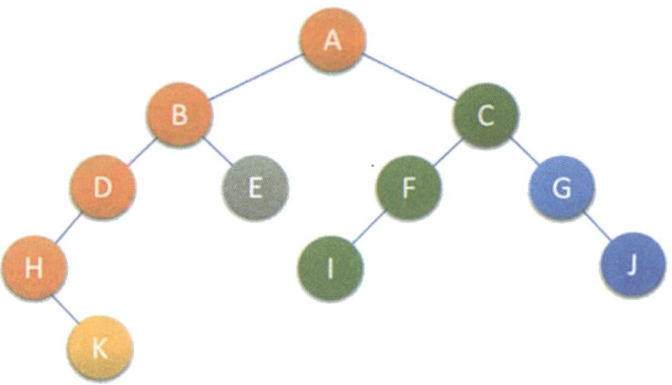
先序遍历结果：ABDHKECFIGJ

代码实现过程：

/* 初始条件: 二叉树T存在 */
/* 操作结果: 前序递归遍历T */
void PreOrderTraverse(BiTree T)
{ 
	if(T==NULL)
		return;
	printf("%c",T->data);/* 显示结点数据，可以更改为其它对结点操作 */
	PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */
	PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */
}

9.2.4 二叉树的中序遍历

中序遍历规则：左根右

中序遍历结果：HKDBEAIFCGJ

代码实现过程：

/* 初始条件: 二叉树T存在 */
/* 操作结果: 中序递归遍历T */
void InOrderTraverse(BiTree T)
{ 
	if(T==NULL)
		return;
	InOrderTraverse(T->lchild); /* 中序遍历左子树 */
	printf("%c",T->data);/* 显示结点数据，可以更改为其它对结点操作 */
	InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */
}

9.2.5 二叉树的后序遍历

后序遍历规则：左右根

后序遍历结果：KHDEBIFJGCA

代码实现过程：

/* 初始条件: 二叉树T存在 */
/* 操作结果: 后序递归遍历T */
void PostOrderTraverse(BiTree T)
{
	if(T==NULL)
		return;
	PostOrderTraverse(T->lchild); /* 先后序遍历左子树  */
	PostOrderTraverse(T->rchild); /* 再后序遍历右子树  */
	printf("%c",T->data);/* 显示结点数据，可以更改为其它对结点操作 */
}

9.2.6 二叉树的层次遍历

层次遍历规则：从上到下

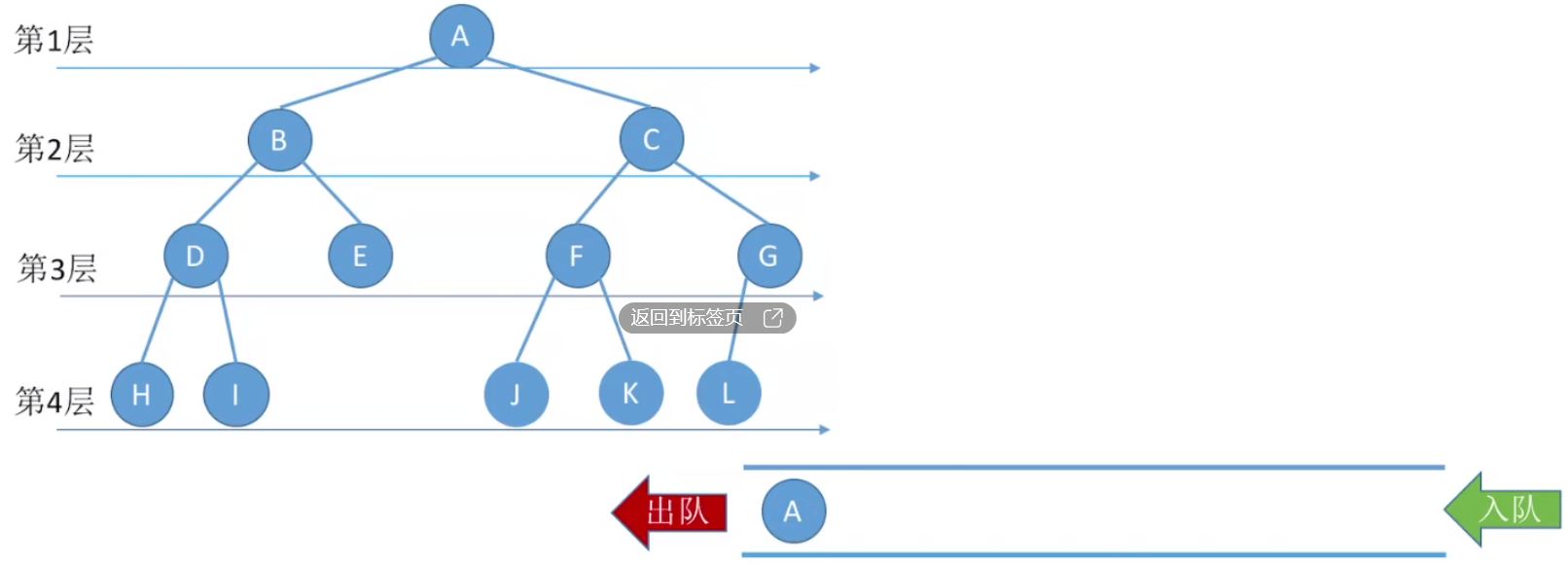
实现思路：

初始化一个辅助的队列
根节点入队
若队列非空，则队头结点出队，访问该结点，并将其左、右孩子插入队尾（如果有的话）

层次遍历结果：ABCDEFGHIJK

代码实现过程：

int LevelOrder(BiTree T)
{
	LinkQueue L;
	BiTree p;

	InitQueue(&L);                 //初始化辅助队列
	EnQueue(&L, T);                //将根节点入队
	while (L.front != L.rear)      //队列不为空则循环
	{
		DeQueue(&L, &p);           //对头结点出队
		printf("%c ", p->data);    //访问出队的结点
		if(p->lchild != NULL)
			EnQueue(&L, p->lchild); //左孩子入队
		if (p->rchild != NULL)
			EnQueue(&L, p->rchild); //右孩子入队
	}
}

9.2.7 二叉树遍历的完整代码

#include "string.h"
#include "stdio.h"  
#include "stdlib.h"   

#define MAXSIZE 100 /* 存储空间初始分配量 */

/* 用于构造二叉树********************************** */
int treeIndex=1;
typedef char String[24]; /*  0号单元存放串的长度 */
String str;

typedef struct BiTNode  /*二叉树结点结构 */
{
	char data;		/* 结点数据 */
	struct BiTNode* lchild, * rchild; /* 左右孩子指针 */
}BiTNode, * BiTree;

typedef struct QNode	/* 链表结点结构 */
{
	BiTree data;
	struct QNode* next;
}QNode, * QueuePtr;

typedef struct			/* 队列的链表结构 */
{
	QueuePtr front, rear; /* 队头、队尾指针 */
}LinkQueue;

int StrAssign(String T,char *chars)
{ 
	int i;
	if(strlen(chars)>MAXSIZE)
		return 0;
	else
	{
		T[0]=strlen(chars);
		for(i=1;i<=T[0];i++)
			T[i]=*(chars+i-1);
		return 1;
	}
}

/* 操作结果: 初始化队列 */
int InitQueue(LinkQueue* L)
{
	L->front = L->rear = (QueuePtr)malloc(sizeof(QNode));
	L->front->next = L->rear->next = NULL;

	return 1;
}

/* 初始条件: 队列L存在 */
/* 操作结果: 把数据入队 */
int EnQueue(LinkQueue* L, BiTree e)
{
	QueuePtr s;

	s = (QueuePtr)malloc(sizeof(QNode));
	s->data = e;
	s->next = NULL;
	L->rear->next = s;
	L->rear = s;

	return 1;
}

/* 初始条件: 队列L存在 */
/* 操作结果: 把数据出队 */
int DeQueue(LinkQueue* L, BiTree* e)
{
	QueuePtr s;

	if (L->front == L->rear)
		return 0;
	s = L->front->next;
	*e = s->data;
	L->front->next = s->next;
	if (L->rear == s)
		L->rear = L->front;
	free(s);

	return 1;
}

/* 从队头到队尾依次对队列Q中每个元素输出 */
int QueueTraverse(LinkQueue Q)
{
	QueuePtr p;
	p = Q.front->next;
	while (p)
	{
		printf("%d ", p->data);
		p = p->next;
	}
	printf("\r\n");

	return 1;
}

/* ************************************************ */
/* 构造空二叉树T */
int InitBiTree(BiTree* T)
{
	*T = NULL;

	return 1;
}

/* 按前序输入二叉树中结点的值（一个字符） */
/* #表示空树，构造二叉链表表示二叉树T。 */
int CreateBiTree(BiTree *T)
{
	char ch;

	ch = str[treeIndex++];

	if (ch == '#')
		*T = NULL;
	else
	{
		*T = (BiTree)malloc(sizeof(BiTNode));
		(*T)->data = ch;
		CreateBiTree(&(*T)->lchild);
		CreateBiTree(&(*T)->rchild);
	}
}

/* 初始条件: 二叉树T存在 */
/* 操作结果: 前序递归遍历T */
void PreOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	printf("%c", T->data);/* 显示结点数据，可以更改为其它对结点操作 */
	PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */
	PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */
}

/* 初始条件: 二叉树T存在 */
/* 操作结果: 中序递归遍历T */
void InOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	InOrderTraverse(T->lchild); /* 中序遍历左子树 */
	printf("%c", T->data);/* 显示结点数据，可以更改为其它对结点操作 */
	InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */
}

/* 初始条件: 二叉树T存在 */
/* 操作结果: 后序递归遍历T */
void PostOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	PostOrderTraverse(T->lchild); /* 先后序遍历左子树  */
	PostOrderTraverse(T->rchild); /* 再后序遍历右子树  */
	printf("%c", T->data);/* 显示结点数据，可以更改为其它对结点操作 */
}

/* 初始条件: 二叉树T存在 */
/* 操作结果: 层次递归遍历T */
int LevelOrder(BiTree T)
{
	LinkQueue L;
	BiTree p;

	InitQueue(&L);                 //初始化辅助队列
	EnQueue(&L, T);                //将根节点入队
	while (L.front != L.rear)      //队列不为空则循环
	{
		DeQueue(&L, &p);           //对头结点出队
		printf("%c", p->data);    //访问出队的结点
		if(p->lchild != NULL)
			EnQueue(&L, p->lchild); //左孩子入队
		if (p->rchild != NULL)
			EnQueue(&L, p->rchild); //右孩子入队
	}
}

int main()
{
	BiTree T;

	InitBiTree(&T);               //初始化一棵树
	StrAssign(str,"ABDH#K###E##CFI###G#J##");
	CreateBiTree(&T);             //建立二叉树
	printf("前序遍历二叉树:");
	PreOrderTraverse(T);
	printf("\r\n中序遍历二叉树:");
	InOrderTraverse(T);
	printf("\r\n后序遍历二叉树:");
	PostOrderTraverse(T);
	printf("\r\n层次遍历二叉树:");
	LevelOrder(T);

	return 0;
}

9.3 线索二叉树

线索二叉树的定义

线索二叉树的存储结构

先序线索二叉树线索化

中序线索二叉树线索化

后序线索二叉树线索化

先序遍历线索二叉树

中序遍历线索二叉树

后序遍历线索二叉树

《大话数据结构》知识点汇总+算法代码总结

注意事项

1. 线性表

1.1 线性表的定义

1.2 线性表的存储结构

1.3 线性表的创建

1.4 线性表的整表创建

1.5 线性表的整表删除

1.6 线性表的插入

1.7 线性表的删除

1.8 线性表的完整代码

2. 单向链表

1.1 单向链表的定义

1.2 单向链表的存储结构

1.3 单向链表的创建

1.4 单向链表的整表的创建

1.4.1 头插法整表创建

1.4.2 尾插法整表创建

1.5 单向链表的整表删除

1.6 单向链表的插入

1.7 单向链表的删除

1.8 单向链表的完整代码

3. 双向链表

1.1 双向链表的定义

1.2 双向链表的存储结构

1.4 双向链表的整表创建

1.4.1 头插法整表创建

1.4.2 尾插法整表创建

1.5 双向链表的整表删除

1.6 双向链表的插入

1.7 双向链表的删除

1.8 双向链表的完整代码

4. 顺序栈

4.1 顺序栈的定义

4.2 顺序栈的存储结构

4.3 顺序栈的创建

4.4 顺序栈的插入

4.5 顺序栈的删除

4.6 顺序栈的完整代码

5. 两栈共享空间

6. 链式栈

4.1 链式栈的定义

4.2 链式栈的存储结构

4.3 链式栈的创建

4.4 链式栈的插入

4.5 链式栈的删除

4.6 链式栈的完整代码

4.7 链式栈的应用 --- 四则运算表达式

4.7.1 定义

4.7.2 中缀表达式转后缀表达式

4.7.3 计算后缀表达式的值

4.7.4 四则运算表达式完整代码

7. 循环顺序队列

7.1 循环顺序队列的定义

7.2 循环顺序队列的存储结构

7.3 循环顺序队列的创建

7.4 循环顺序队列的插入

7.5 循环顺序队列的删除

7.6 循环顺序队列的完整代码

8.链式队列

8.1 链式队列的定义

8.2 链式队列的存储结构

8.3 链式队列的创建

8.4 链式队列的插入

8.5 链式队列的删除

8.6 链式队列的完整代码

9. 树

9.1 树的定义

9.2 二叉树

9.2.1 二叉树的定义

9.2.2 二叉树的存储结构

9.2.3 二叉树的建立

9.2.3 二叉树的先序遍历

9.2.4 二叉树的中序遍历

9.2.5 二叉树的后序遍历

9.2.6 二叉树的层次遍历

9.2.7 二叉树遍历的完整代码

9.3 线索二叉树

评论区